<h1>Assessing the validity of item response theory models when calibrating field test items</h1>
<h2>Brandon LeBeau</h2>
<h3>University of Iowa</h3>
# Validity for IRT Models
- Validity is important for any assessment and the argument should begin with psychometrics.
- How the psychometrics is performed directly impacts properties of the assessment that are assessed later for evidence of validity.
+ Are scores reported below chance level?
- The validity of the psychometrics is particularly important for field test data.
# IRT Model
<img src="/figs/irt.PNG" alt="" height = "200" width="1200"/>
# Field Testing
- Field testing (FT) is essential to new assessment development or form building.
+ A way to gather information to make informed decisions about which items become operational.
- Limitations:
+ Many items are tried that do not become operational.
- This spreads a fixed pool of individuals (respondents) across many field test items.
- Ultimately, sample size can be significantly smaller compared to operational assessments.
+ Issues with distractors.
# Threats to Validity in FT
- Generalizeability
+ Is the FT sample representative of the desired population?
+ Over-fitting with 3PL model?
- Uncertainty in estimates
+ Sample size and lower asymptote estimation
+ Interconnected parameter estimates
# Generalizeability
- We assume respondents are randomly sampled from some population.
+ Are item responses truly randomly sampled from the population of interest?
- Selection or Measurement bias
+ If not, estimates are extremely sample dependent.
- 3PL model may provide better fit, but is this at the cost of overfitting?
+ Fit should not be the only consideration when deciding on an IRT model for FT data.
# Uncertainty
- Sample size (1000 commonly cited for 3PL model):
+ Tends to be smaller in field test designs.
+ Even with small samples, can achieve convergence with 3PL model with help of priors, ridge, etc.
- Are our estimates now biased?
- Estimating Lower Asymptote (pseudo-guessing):
+ Difficulty in estimating this term ($c_{j}$) has direct impact on estimation of the other two terms.
- This leads to a cascading vortex of problems.
+ The pseudo-guessing is commonly a nuisance parameter, why allow a nuisance parameter to drastically affect estimation of other terms?
# Methodology
- Individual response strings were resampled in a two stage framework:
+ First, individuals who took the field test were resampled with replacement within each field test booklet.
+ Second, individuals who only took operational items were resampled with replacement to fill out the remaining observations.
- After resampling, items were calibrated with Bilog-MG.
- This process was replicated 5000 times to generate bootstrapped item parameters.
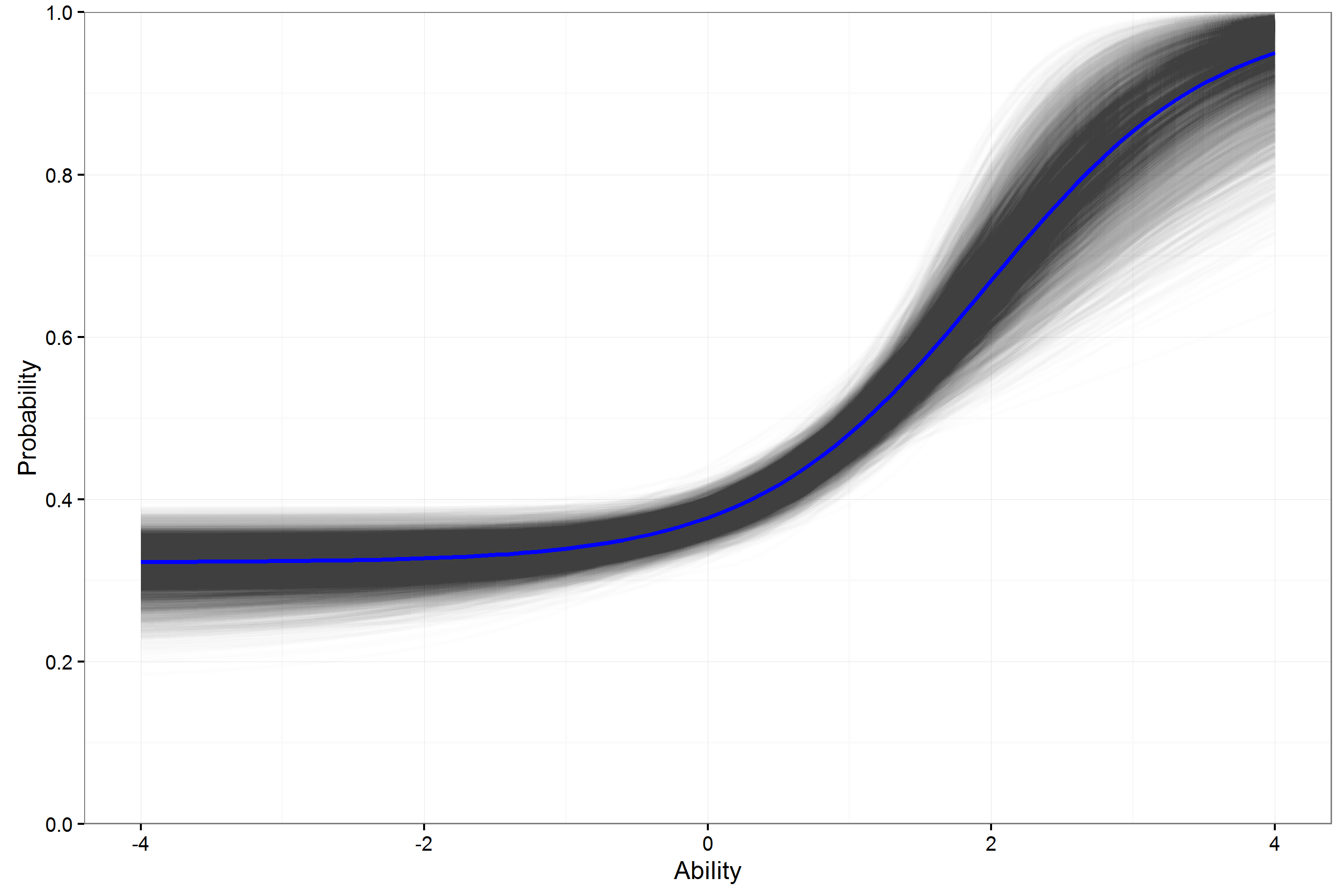
# Example ICC Math FT Item 3PL
<img src="/figs/iccgr3math57.png" alt="" height = "500" width="1200"/>
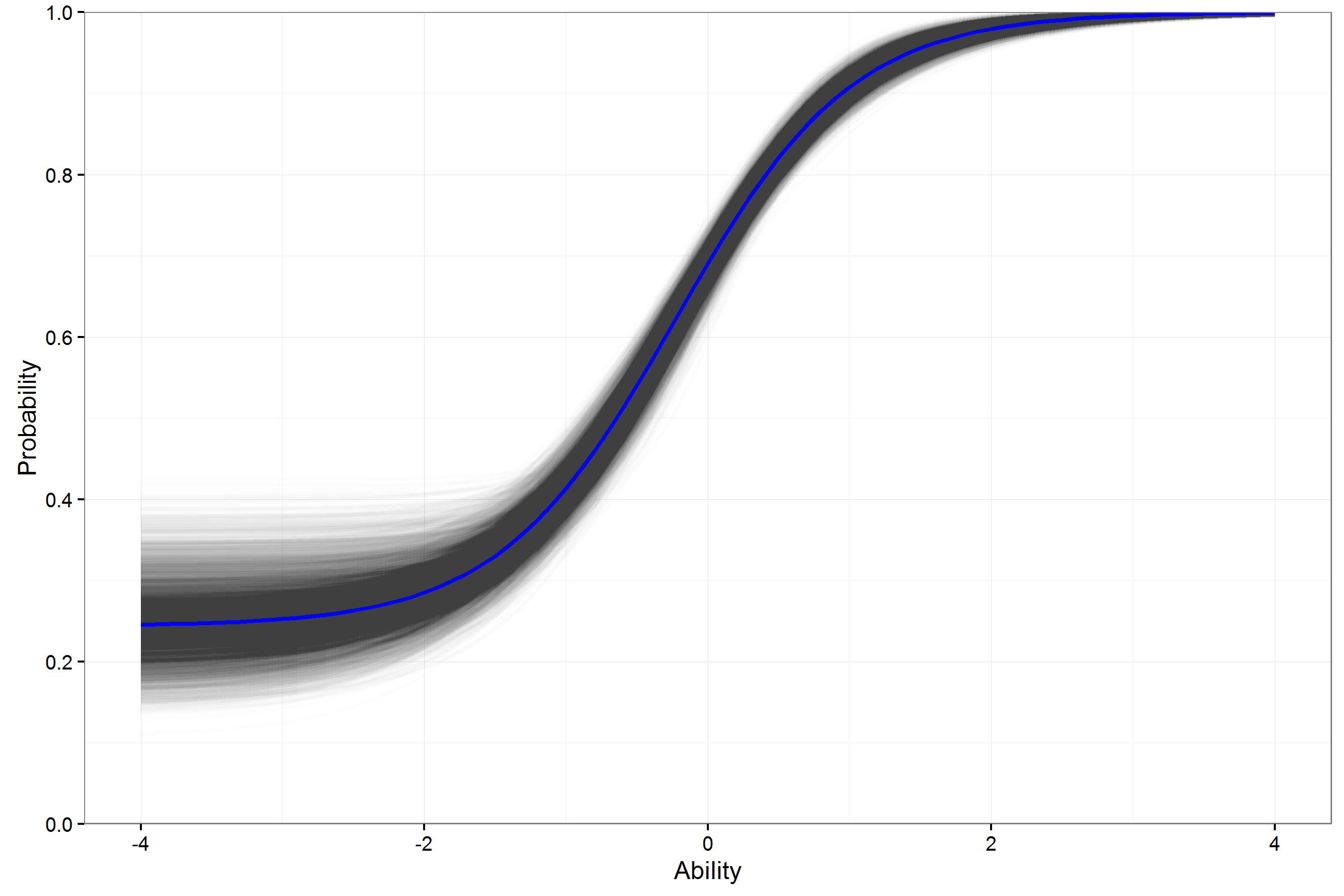
# Example ICC Math FT Item 2PL
<img src="/figs/iccgr3math572pl.png" alt="" height = "500" width="1200"/>
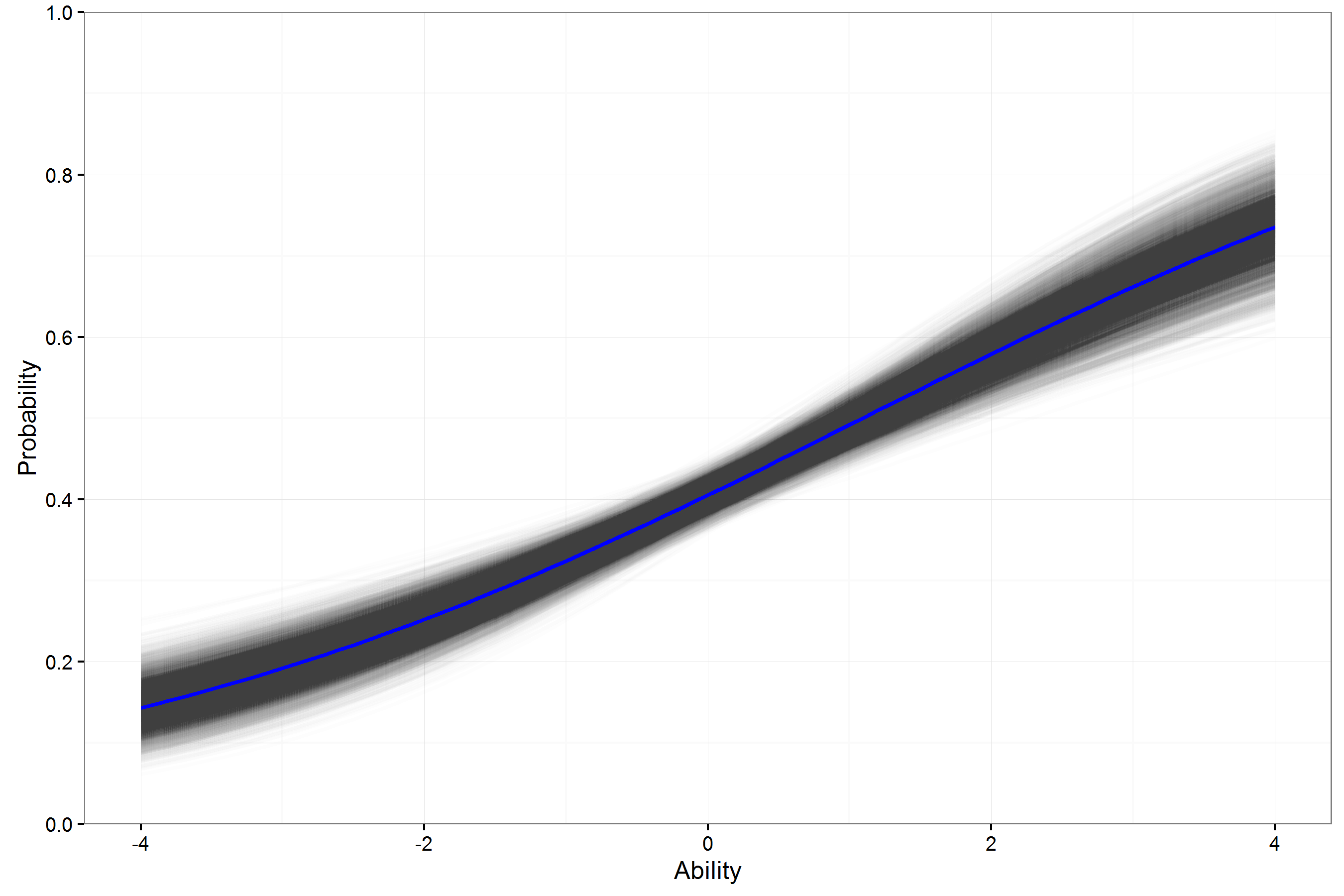
# Example ICC ELA FT Item 3PL
<img src="/figs/iccread653pl.png" alt="" height = "500" width="1200"/>
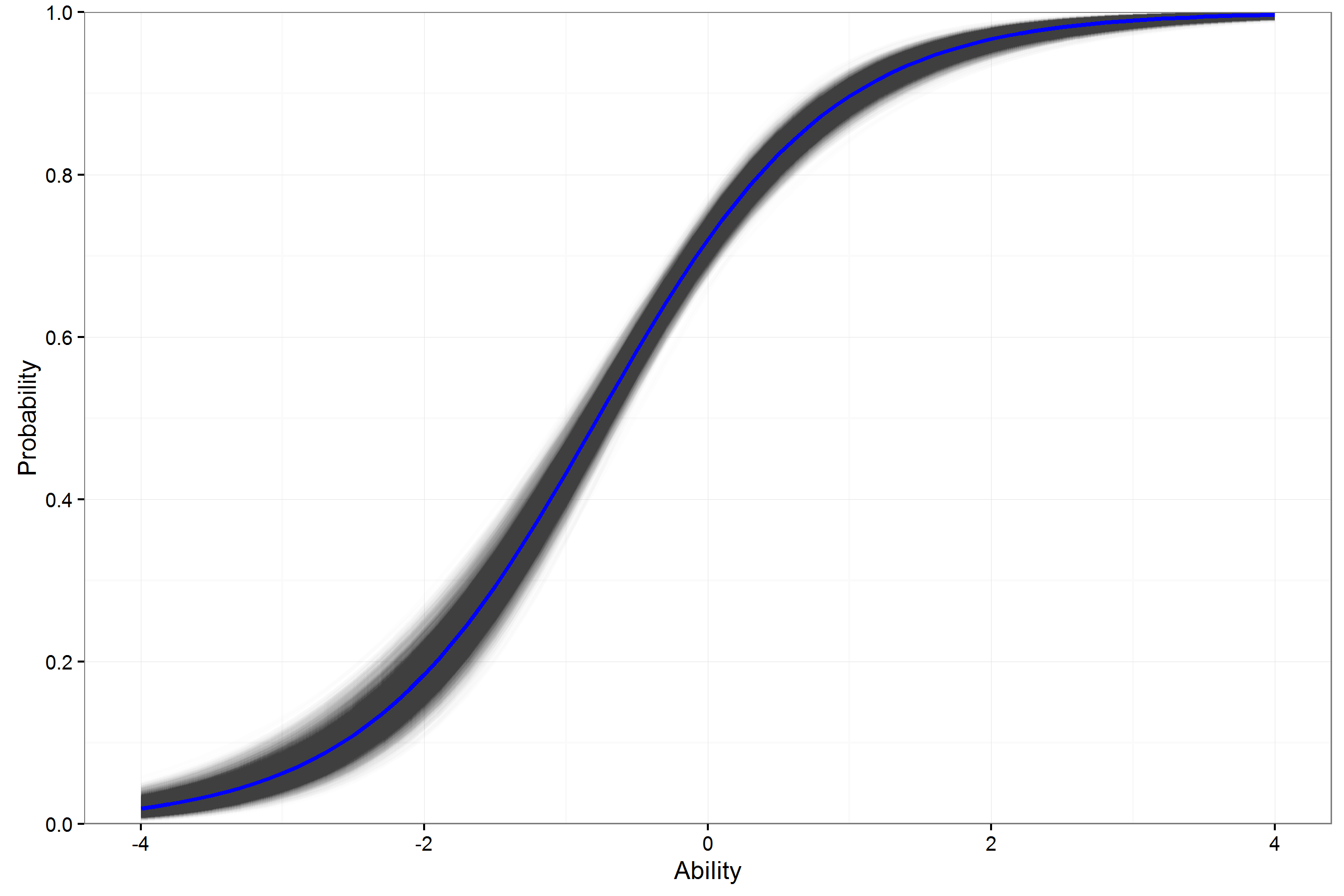
# Example ICC ELA FT Item 2PL
<img src="/figs/iccread652pl.png" alt="" height = "500" width="1200"/>
# ICC Summary
- For individual items, the variation in the ICCs for a 3PL model can be large.
+ This may lower usefulness of estimates in helping to select operational (best) items.
- How can these 3PL curves be expected to generalize beyond this sample with so much variability?
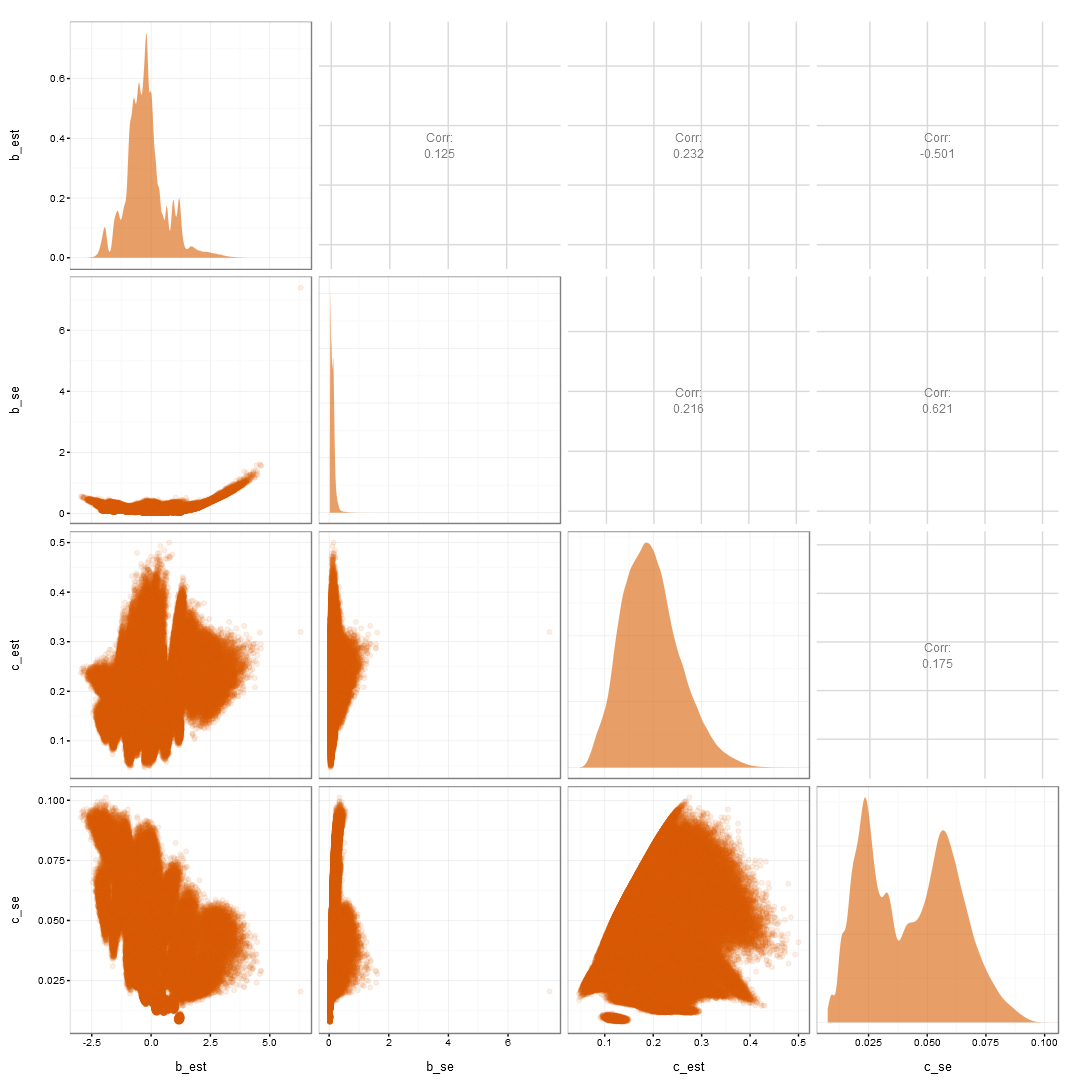
# b and c est and SE
<img src="/figs/pairs_bc_ela.png" alt="" height = "500" width="1200"/>
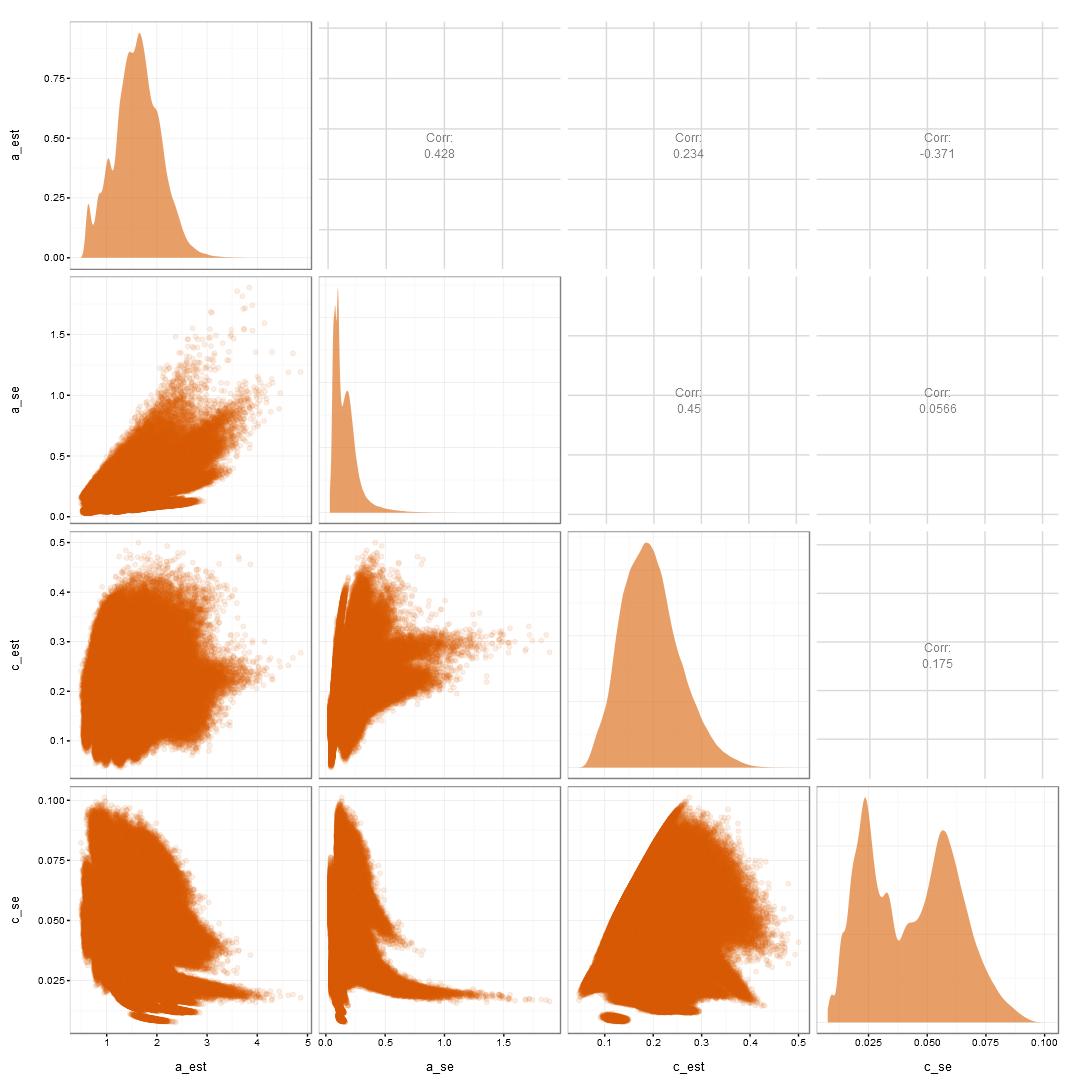
# a and c est and SE
<img src="/figs/pairs_ac_ela.png" alt="" height = "500" width="1200"/>
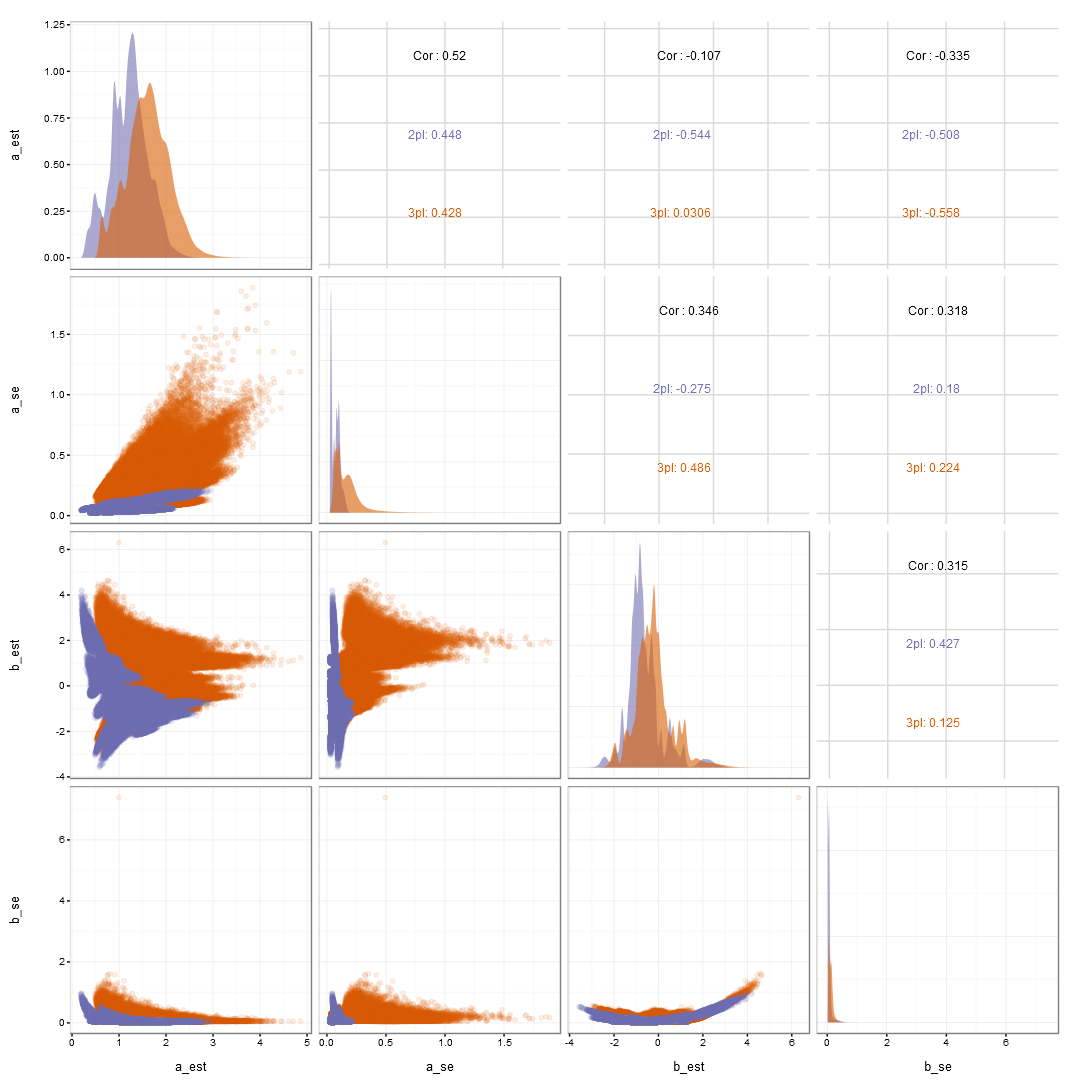
# a and b est and SE
<img src="/figs/pairs_ab_ela.png" alt="" height = "500" width="1200"/>
# Uncertainty Summary
- The pseudo-guessing estimates are:
+ negatively related to the estimates of the b and a.
+ positively related to the uncertainty in the b parameter, likely the parameter of most interest.
- In turn, increasing the uncertainty in the b parameter:
+ further increases the uncertainty in the a parameter.
+ is also negatively related to estimates of the a parameter.
- Thus, creating the cascading vortex of problems.
# Conclusions
- Item parameters estimated from FT data should not be treated as truth.
+ Variation in these parameter estimates needs to be considered.
- Fit should not be the only concern when selecting an IRT model, uncertainty, generalizeability, and usefulness should also be considered.
- Estimates are much more stable when using the 2PL model.
+ Thus providing a stronger foundation with which to start the validity argument for an assessment.
# Questions?
- Twitter: @blebeau11
- Website: <http://brandonlebeau.org> <br/> <http://www2.education.uiowa.edu/directories/person?id=bleb>
- Slides: <http://brandonlebeau.org/2016/04/09/ncme2016.html>