Linking with the Bayesian Item Response Theory Model

Brandon LeBeau & Xiaoting Zhong

2023-03-30

Research Problem

  • IRT models specified as linear mixed models are not new (e.g., Adams, Wilson, & Wu, 1997; Kamata, 2001; Mellenbergh, 1994; Rijmen et al., 2003).
  • Some have discussed evaluating DIF in these frameworks too (e.g., Noorgate and De Boeck, 2005).
  • To our knowledge, these methods have not been explored to which the extent they properly link scores.

Heterotypic Continuity

  • We approach this research primarily from a psychological measurement lens, where heterotypic continuity is often of concern.
  • Heterotypic Continuity occurs when the same psychological reasons underlie different behaviors at different ages—the same construct looks different across development (Petersen, Choe & LeBeau, 2020).
  • Examples: Externalizing Problems (Petersen & LeBeau, 2020; Petersen & LeBeau, 2021)

Limitations of current linking

  • Item parameter estimates treated as known parameters for linking.
    • Problematic in small samples
  • Does not account for any clustering in the data collection design
  • Current software for linking is cumbersome to use.
    • Limits use for applied researchers

Bayesian Generalized Linear Mixed Model

Focusing on dichotomous items, we could define a 2pl IRT model within a linear mixed model:

\[ P(y = 1) = logistic(\alpha_{i}(b_{p} + \gamma_{i})) \]

  • \(\alpha_{i}\) is item specific discrimination
  • \(b_{p}\) is a random person effect, often called theta or ability
  • \(\gamma_{i}\) is an item easiness term

Adding Attributes

Attributes can be added as item, person, or both item and person attributes.

Example:

\[ P(y = 1) = logistic(\alpha_{i}(b_{p} + \gamma_{i} + X_{jpi} \beta_{j})) \]

  • \(X_{jpi}\) is a design matrix.
  • \(\beta_{j}\) are a set of \(J\) regression coefficients.

Specific Example - 3 time points

Example

\[ P(y = 1) = logistic(\alpha_{i}(b_{p} + \gamma_{i} + \beta_{1} time_{2} + \beta_{2} time_{3})) \]

  • \(time_{2}\) is a dummy attribute, 1 = time 2, 0 = otherwise
  • \(time_{3}\) is a dummy attribute, 1 = time 3, 0 = otherwise

Simulation Conditions

  • Sample size fixed at 1000
  • 3 time points
  • Number of items fixed at 20 for each time point
  • 10 common items (40 total items, 10 in common, 10 unique across 3 time points)
  • Change in common easiness: -0.5, 0, 0.5

Data Generation

  • Data were generated by randomly generating 1000 person parameters (ability/theta)
  • Item parameter were randomly generated for all unique items (30 items)
  • Common item parameters at each time point were shifted based on the change in common easiness.

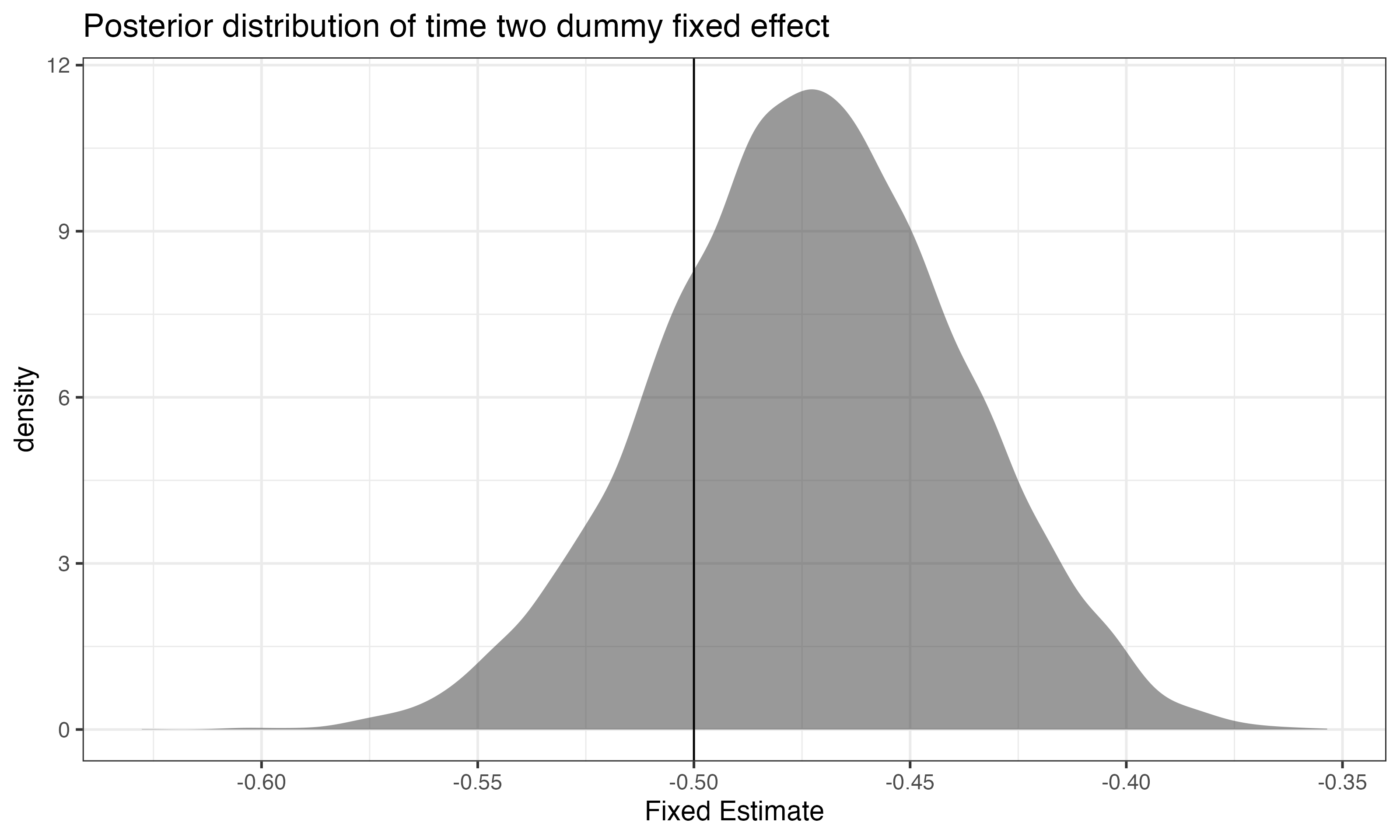
Fixed Effect Results - Time 2

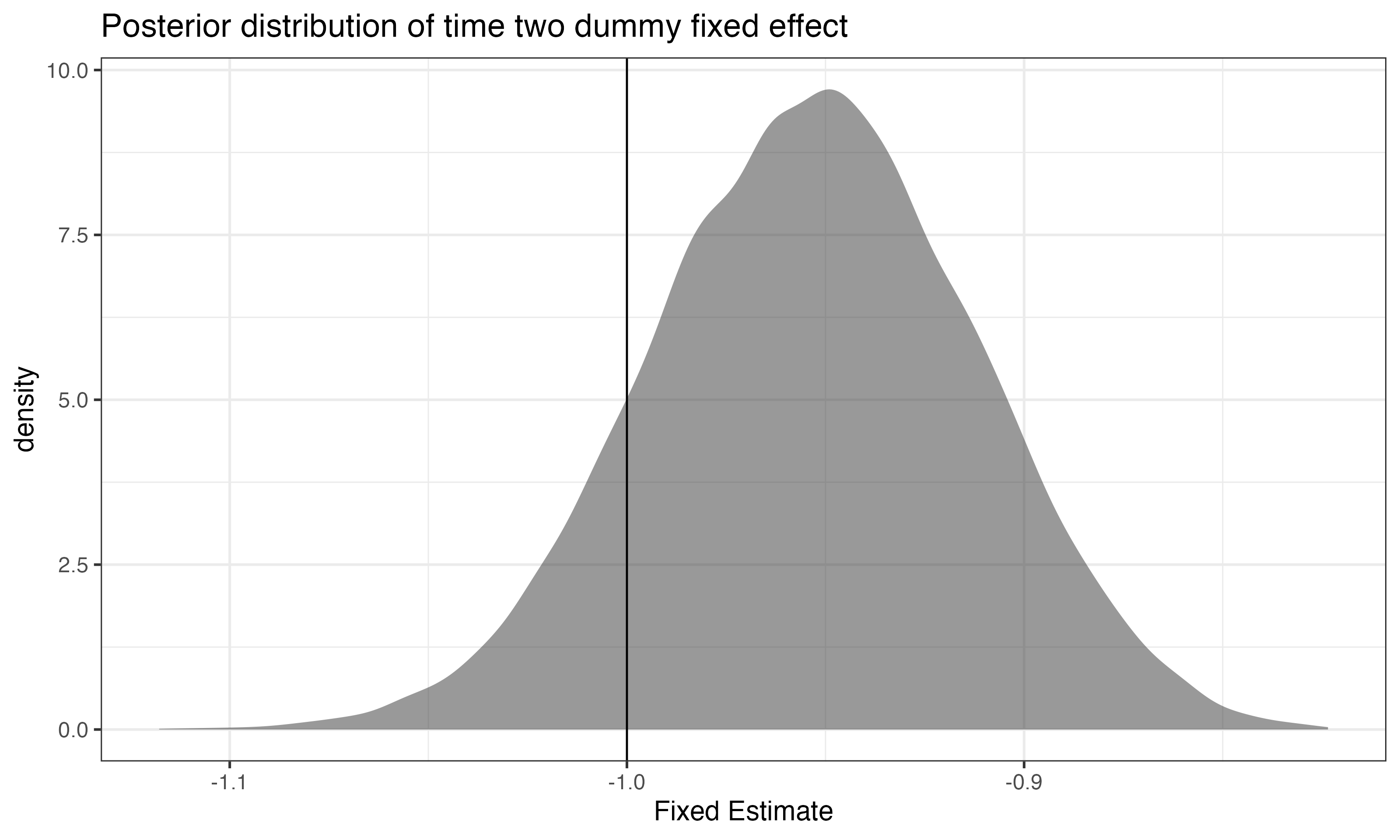
Fixed Effect Results - Time 3

Recovering Ability

Concluding Remarks

  • Fitting IRT models as mixed models is highly flexible.
  • Preliminary evidence suggests adequate recovery of parameters.
  • May work in small samples due to ability to impose prior information

Future Work

  • Vary more data conditions to evaluate ability to link across different situations
    • Non-linear change across time
    • More time points
    • Smaller sample size
  • Evaluate more complex model to allow variance of person parameters to change over time

Get in Touch