<h1>Simulation and Power Analysis of Generalized Linear Mixed Models</h1>
<h2>Brandon LeBeau</h2>
<h3>University of Iowa</h3>
# Overview
1. Power
2. `simglm` package
3. Shiny Demo
# Power
- Power is the ability to statistically detect a true effect (i.e. non-zero population effect).
- For simple models (e.g. t-tests, regression) there are closed form equations for generating power.
+ R has routines for these: `power.t.test, power.anova.test`
+ Gpower3
# Power Example
```r
n <- seq(20, 1000, 5)
power <- sapply(seq_along(n), function(i)
power.t.test(n = n[i], delta = .15, sd = 1, type = 'two.sample')$power)
```
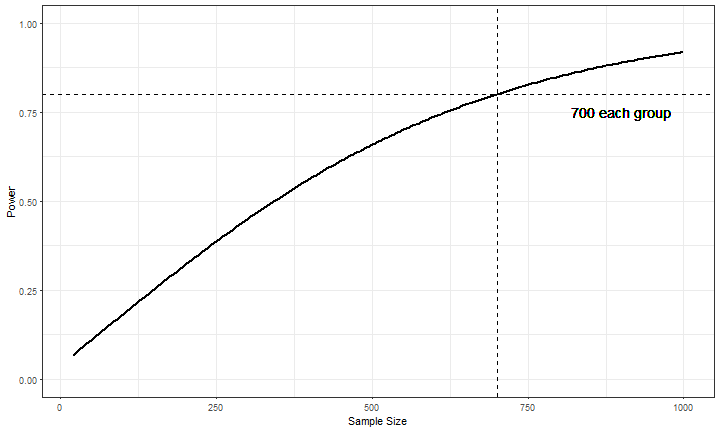
# Power for (G)LMM
- Power for more complex models is not as straightforward;
+ particularly with messy real world data.
- There is software for GLMM models to generate power
+ Optimal Design: <http://hlmsoft.net/od/>
+ MLPowSim: <http://www.bristol.ac.uk/cmm/software/mlpowsim/>
+ Snijders, *Power and Sample Size in Multilevel Linear Models*.
+ Moerbeek & Teerenstra, *Power Analysis of Trials with Multilevel Data*.
# Power is hard
- In practice, power is hard.
- Need to make many assumptions on data that has not been collected.
+ Therefore, data assumptions made for power computations will likely differ from collected sample.
- A power analysis needs to be flexible, exploratory, and well thought out.
# Why do power?
- Three common reasons to do power analysis:
1. Power evidence for grant/planning
2. Post Hoc to explore insignificant results
3. Monte Carlo studies
# `simglm` Features
* Longitudinal data simulation
* Three levels of nesting
* Specification of distribution of random components (random effects and random error)
* Specification of serial correlation
* Specification of the number of variables
+ Ability to add time-varying covariates
+ Specify the mean and variance of fixed covariate variables
+ Factor variable simulation
+ Ordinal variable simulation
# `simglm` Features Continued
* Power by simulation
+ Vary parameters for a factorial simulation design.
+ Can vary model fitted to the data to misspecify directly.
* Simulation of missing data
* Include other distributions for covariate simulation.
* Continuous, Logistic (dichotomous), and Poisson (count) outcome variables.
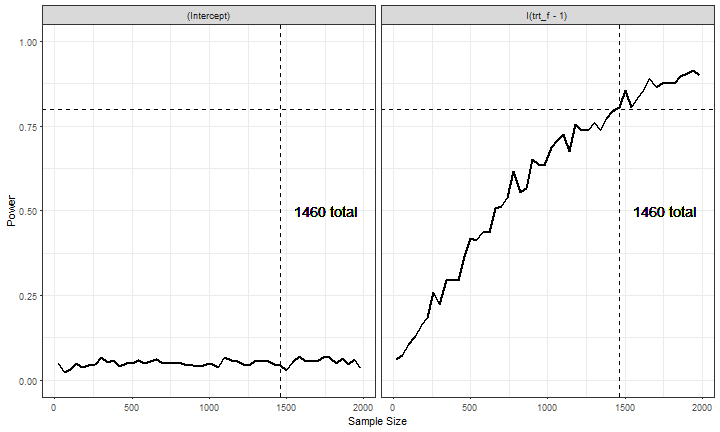
# Replicate with `simglm`
* Note this code uses the development version on GitHub
```r
library(simglm)
fixed <- ~ 1 + trt_f
fixed_param <- c(0, 0.15)
fact_vars <- list(numlevels = 2, var_type = 'single',
opts = list(list(replace = TRUE)))
n <- NULL
error_var <- 1
with_err_gen <- 'rnorm'
pow_param <- c('(Intercept)', 'I(trt_f - 1)')
alpha <- .05
pow_dist <- "t"
pow_tail <- 2
replicates <- 500
terms_vary <- list(n = seq(20, 2000, 40))
power_out <- sim_pow(fixed = fixed, fixed_param = fixed_param, cov_param = NULL,
n = n, error_var = error_var, with_err_gen = with_err_gen,
fact_vars = fact_vars,
data_str = "single", pow_param = pow_param, alpha = alpha,
pow_dist = pow_dist, pow_tail = pow_tail,
replicates = replicates, terms_vary = terms_vary,
raw_power = FALSE, lm_fit_mod = sim_data ~ I(trt_f - 1))
```
# Plot Results
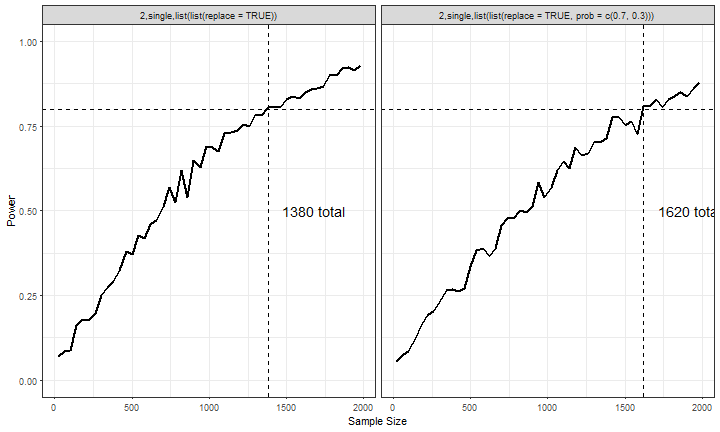
# More Realistic?
```r
terms_vary <- list(n = seq(20, 2000, 40),
fact_vars = list(list(numlevels = 2, var_type = 'single',
opts = list(list(replace = TRUE))),
list(numlevels = 2, var_type = 'single',
opts = list(list(replace = TRUE,
prob = c(.7, .3))))))
pow_param <- c('I(trt_f - 1)')
power_out <- sim_pow(fixed = fixed, fixed_param = fixed_param, cov_param = NULL,
n = n, error_var = error_var, with_err_gen = with_err_gen,
fact_vars = fact_vars,
data_str = "single", pow_param = pow_param, alpha = alpha,
pow_dist = pow_dist, pow_tail = pow_tail,
replicates = replicates, terms_vary = terms_vary,
raw_power = FALSE, lm_fit_mod = sim_data ~ I(trt_f - 1))
```
# Results
# Shiny Demo
- Once the package is installed, can run the Shiny app locally.
```r
run_shiny()
```
# Connect
- Twitter: @blebeau11
- Website: <https://brandonlebeau.org>
- Slides: <https://brandonlebeau.org/slides/jsm2017.html>
- GitHub: <http://github.com/lebebr01/simglm>