simglm v0.9.26: Multi-level Propensity Score Modeling

R
simglm
modeling
propensity scores
Author

Brandon LeBeau

Published

November 6, 2025

This update marks the final propensity score enhancement for the simglm package (v0.9.26). It introduces multi-level propensity score modeling, enabling users to simulate data with nested structures and treatment effects that vary across levels.

Propensity score methods often assume independence between units, but in real-world settings, data are hierarchical (e.g., students nested in classrooms, patients nested in hospitals). This release bridges that gap—allowing for realistic multi-level causal inference simulation.

🆕 New Features at a Glance

  • Hierarchical data simulation — Generate nested structures (e.g., students within schools, hospitals within regions).
  • Multi-level propensity modeling — The propensity_model argument now supports random effects and hierarchical assignment.
  • Cross-level treatment effects — Specify treatments applied at any level (e.g., classrooms, schools, or districts).
  • Custom model fitting functions — Pass your own model-fitting function (glm, lme4::glmer, or even brms::brm) with additional arguments.

If you haven’t already, remember to first install the latest release of the simglm package from GitHub.

Code 
remotes::install_github('lebebr01/simglm')

Multi-level Propensity Score Modeling Example

First, let’s show the new features that allow the user to specify a multi-level propensity score model. In this example, we will simulate data with students nested within classrooms, where the treatment assignment is still being specified at the student level. The model formula specified for both the full data generation and propensity model specification use lme4 style syntax. Any data features generated during the propensity score model simulation carry over to the final data generation step.

Code 
library(simglm)

level1_samp <- sample(15:25, size = 50, replace = TRUE)

sim_arguments <- list(
    formula = achievement ~ 1 + motivation + trt + age + ses + (1 | classroom),
    fixed = list(
        motivation = list(var_type = 'continuous',
                           mean = 0, sd = 20)
    ),
    sample_size = list(level1 = level1_samp, level2 = 50),
    error = list(variance = 10),
    reg_weights = c(50, 0.4, 1.2, 0.1, 0.25),
    randomeffect = list(int_classroom = list(variance = 5, var_level = 2)),
    propensity = list(
        formula = trt ~ 1 + age + ses + (1 | classroom),
        fixed = list(age = list(var_type = 'ordinal', 
                         levels = -7:7),
                     ses = list(var_type = 'continuous', 
                         mean = 0, sd = 5, 
                         var_level = 2)),
        sample_size = list(level1 = level1_samp, level2 = 50),
        error = list(variance = 5),
        randomeffect = list(int_classroom = list(variance = 5, var_level = 2)),
        reg_weights = c(2, 0.3, -0.5),
        outcome_type = 'binary'
    )
)
simulate_fixed(data = NULL, sim_args = sim_arguments) |>
    simulate_error(sim_args = sim_arguments) |>
    simulate_randomeffect(sim_args = sim_arguments) |>
    generate_response(sim_arguments) |> 
    head()
  X.Intercept. motivation trt age      ses level1_id classroom      error
1            1   6.502731   1  -4 1.026945         1         1 -0.9554712
2            1   4.548620   1   2 1.026945         2         1 -5.7521228
3            1  11.132905   0  -2 1.026945         3         1  3.8836490
4            1  -3.523738   0   2 1.026945         4         1  1.6403897
5            1  41.977955   0  -3 1.026945         5         1 -2.5984848
6            1  -8.826909   0  -6 1.026945         6         1 -0.0853880
  int_classroom fixed_outcome random_effects achievement
1     -1.405126      53.65783      -1.405126    51.29723
2     -1.405126      53.47618      -1.405126    46.31894
3     -1.405126      54.50990      -1.405126    56.98842
4     -1.405126      49.04724      -1.405126    49.28251
5     -1.405126      66.74792      -1.405126    62.74431
6     -1.405126      46.12597      -1.405126    44.63546

Specifying treatment at different levels

In addition to specifying treatment at level 1 (e.g., students), users can now specify treatment assignment at higher levels (e.g., classrooms). Below is an example where treatment is assigned at level 2 (classrooms). The simglm package does this by computing the average value for each cluster (classrooms here) and then uses that value to assign the treatment to that cluster. To specify this treatment assignment, the user simply needs to set the outcome_level argument within the propensity list to the desired level (2 in this case).

Code 
level1_samp <- sample(15:25, size = 50, replace = TRUE)

sim_arguments <- list(
    formula = achievement ~ 1 + motivation + trt + age + ses + (1 | classroom),
    fixed = list(
        motivation = list(var_type = 'continuous',
                           mean = 0, sd = 20)
    ),
    sample_size = list(level1 = level1_samp, level2 = 50),
    error = list(variance = 10),
    reg_weights = c(50, 0.4, 1.2, 0.1, 0.25),
    randomeffect = list(int_classroom = list(variance = 5, var_level = 2)),
    propensity = list(
        formula = trt ~ 1 + age + ses + (1 | classroom),
        fixed = list(age = list(var_type = 'ordinal', 
                         levels = -7:7),
                     ses = list(var_type = 'continuous', 
                         mean = 0, sd = 5, 
                         var_level = 2)),
        sample_size = list(level1 = level1_samp, level2 = 50),
        error = list(variance = 5),
        randomeffect = list(int_classroom = list(variance = 5, var_level = 2)),
        reg_weights = c(2, 0.3, -0.5),
        outcome_type = 'binary',
        outcome_level = 2
    )
)
simulate_fixed(data = NULL, sim_args = sim_arguments) |>
    simulate_error(sim_args = sim_arguments) |>
    simulate_randomeffect(sim_args = sim_arguments) |>
    generate_response(sim_arguments)|> 
    head()
  X.Intercept. motivation trt age       ses level1_id classroom      error
1            1  23.948833   1   2 -1.499993         1         1 -3.4630538
2            1   3.517415   1   5 -1.499993         2         1  1.0019384
3            1 -12.423001   1   4 -1.499993         3         1  0.4293656
4            1 -23.844401   1  -6 -1.499993         4         1 -0.9232922
5            1 -44.794205   1   3 -1.499993         5         1  1.9578812
6            1  14.122256   1  -5 -1.499993         6         1 -2.1116858
  int_classroom fixed_outcome random_effects achievement
1      5.951099      60.60453       5.951099    63.09258
2      5.951099      52.73197       5.951099    59.68500
3      5.951099      46.25580       5.951099    52.63627
4      5.951099      40.68724       5.951099    45.71505
5      5.951099      33.20732       5.951099    41.11630
6      5.951099      55.97390       5.951099    59.81332

💡 Tip: When treatment is assigned at a higher level, all units within that cluster receive the same treatment indicator. This makes simulation results especially useful for cluster-randomized trial designs.

Visualization Example

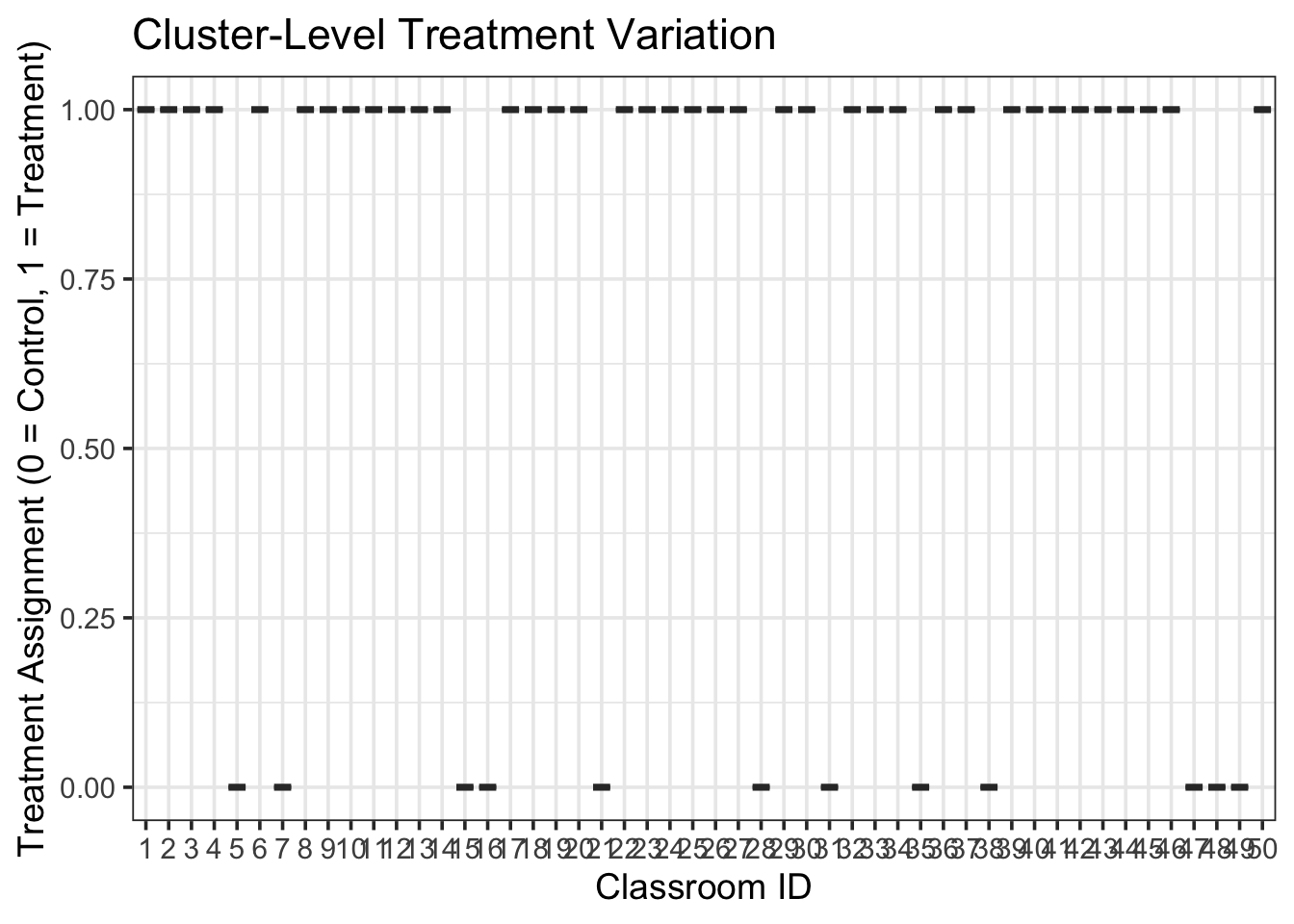
Here’s a quick example of how you might visualize simulated treatment variation across classrooms:

Code 
sim_data <- simulate_fixed(data = NULL, sim_args = sim_arguments) |>
  simulate_error(sim_args = sim_arguments) |>
  simulate_randomeffect(sim_args = sim_arguments) |>
  generate_response(sim_arguments)

ggplot(sim_data, aes(x = factor(classroom), y = trt)) +
  geom_boxplot() +
  labs(
    x = "Classroom ID",
    y = "Treatment Assignment (0 = Control, 1 = Treatment)",
    title = "Cluster-Level Treatment Variation"
  )

Three-level Example

Here is an example where there are now classrooms and districts being specified. The treatment assignment is still being specified at the classroom level with outcome_level = 2, but there is now another level to be considered.

Code 
level1_samp <- sample(15:25, size = 150, replace = TRUE)

sim_arguments <- list(
    formula = achievement ~ 1 + motivation + trt + age + ses + (1 | classroom) + (1 | district),
    fixed = list(
        motivation = list(var_type = 'continuous',
                           mean = 0, sd = 20)
    ),
    sample_size = list(level1 = level1_samp, level2 = 10, level3 = 15),
    error = list(variance = 10),
    reg_weights = c(50, 0.4, 1.2, 0.1, 0.25),
    randomeffect = list(int_classroom = list(variance = 5, var_level = 2),
    int_district = list(variance = 2, var_level = 3)),
    propensity = list(
        formula = trt ~ 1 + age + ses + (1 | classroom) + (1 | district),
        fixed = list(age = list(var_type = 'ordinal', 
                         levels = -7:7),
                     ses = list(var_type = 'continuous', 
                         mean = 0, sd = 5, 
                         var_level = 2)),
        sample_size =  list(level1 = level1_samp, level2 = 10, level3 = 15),
        error = list(variance = 5),
        randomeffect = list(int_classroom = list(variance = 5, var_level = 2),
        int_district = list(variance = 2, var_level = 3)),
        reg_weights = c(2, 0.3, -0.5),
        outcome_type = 'binary',
        outcome_level = 2
    )
)
simulate_fixed(data = NULL, sim_args = sim_arguments) |>
    simulate_error(sim_args = sim_arguments) |>
    simulate_randomeffect(sim_args = sim_arguments) |>
    generate_response(sim_arguments) |> 
    head()
New names:
New names:
• `X.Intercept.` -> `X.Intercept....1`
• `X.Intercept.` -> `X.Intercept....2`
  X.Intercept. motivation trt age       ses level1_id classroom district
1            1 -54.488721   1  -1 -5.700812         1         1        1
2            1  -5.005362   1  -1 -5.700812         2         1        1
3            1  37.278043   1  -2 -5.700812         3         1        1
4            1 -20.904998   1   5 -5.700812         4         1        1
5            1  12.779405   1  -7 -5.700812         5         1        1
6            1   4.861477   1  -7 -5.700812         6         1        1
      error int_classroom int_district fixed_outcome random_effects achievement
1 -7.056390      1.836647    0.2612293      27.87931       2.097876    22.92079
2 -4.276418      1.836647    0.2612293      47.67265       2.097876    45.49411
3  4.207792      1.836647    0.2612293      64.48601       2.097876    70.79168
4  3.465661      1.836647    0.2612293      41.91280       2.097876    47.47634
5  2.112933      1.836647    0.2612293      54.18656       2.097876    58.39737
6 -1.283107      1.836647    0.2612293      51.01939       2.097876    51.83416

Treatment assignment at level 3

The treatment assignment can alternatively be specified at the district level, by setting outcome_level = 3 within the propensity list.

Code 
level1_samp <- sample(15:25, size = 150, replace = TRUE)

sim_arguments <- list(
    formula = achievement ~ 1 + motivation + trt + age + ses + (1 | classroom) + (1 | district),
    fixed = list(
        motivation = list(var_type = 'continuous',
                           mean = 0, sd = 20)
    ),
    sample_size = list(level1 = level1_samp, level2 = 10, level3 = 15),
    error = list(variance = 10),
    reg_weights = c(50, 0.4, 1.2, 0.1, 0.25),
    randomeffect = list(int_classroom = list(variance = 5, var_level = 2),
    int_district = list(variance = 2, var_level = 3)),
    propensity = list(
        formula = trt ~ 1 + age + ses + (1 | classroom) + (1 | district),
        fixed = list(age = list(var_type = 'ordinal', 
                         levels = -7:7),
                     ses = list(var_type = 'continuous', 
                         mean = 0, sd = 5, 
                         var_level = 2)),
        sample_size =  list(level1 = level1_samp, level2 = 10, level3 = 15),
        error = list(variance = 5),
        randomeffect = list(int_classroom = list(variance = 5, var_level = 2),
        int_district = list(variance = 2, var_level = 3)),
        reg_weights = c(2, 0.3, -0.5),
        outcome_type = 'binary',
        outcome_level = 3
    )
)
simulate_fixed(data = NULL, sim_args = sim_arguments) |>
    simulate_error(sim_args = sim_arguments) |>
    simulate_randomeffect(sim_args = sim_arguments) |>
    generate_response(sim_arguments)|> 
    head()
New names:
New names:
• `X.Intercept.` -> `X.Intercept....1`
• `X.Intercept.` -> `X.Intercept....2`
  X.Intercept. motivation trt age      ses level1_id classroom district
1            1  -4.538476   1   7 1.670979         1         1        1
2            1  -9.869254   1   3 1.670979         2         1        1
3            1  -6.006584   1   3 1.670979         3         1        1
4            1  16.765529   1   2 1.670979         4         1        1
5            1  -9.933779   1  -3 1.670979         5         1        1
6            1  34.817235   1   5 1.670979         6         1        1
       error int_classroom int_district fixed_outcome random_effects
1  1.7127887      4.874151     -0.98758      50.50235       3.886571
2 -2.5383693      4.874151     -0.98758      47.97004       3.886571
3  0.3557401      4.874151     -0.98758      49.51511       3.886571
4 -3.2642383      4.874151     -0.98758      58.52396       3.886571
5  1.2402380      4.874151     -0.98758      47.34423       3.886571
6 -5.6804034      4.874151     -0.98758      66.04464       3.886571
  achievement
1    56.10171
2    49.31824
3    53.75742
4    59.14629
5    52.47104
6    64.25081

Flexible Model Specification

The other enhancement is to how the propensity model is fitted and extracted. The internal function for this process has been generalized to allow users to specify whichever model fitting procedure they want. If no model fitting is specified, stats::glm() function is used. If there is a multi-level structure, lme4::glmer() or some alternative, would be more appropriate and would need to be specified within the propensity_model simulation arguments.

Code 
level1_samp <- sample(15:25, size = 75, replace = TRUE)

sim_arguments <- list(
    formula = achievement ~ 1 + motivation + trt + age + ses + (1 | classroom),
    fixed = list(
        motivation = list(var_type = 'continuous',
                           mean = 0, sd = 20)
    ),
    sample_size = list(level1 = level1_samp, level2 = 75),
    error = list(variance = 10),
    reg_weights = c(0, 0.4, 1.2, 0.1, 0.25),
    randomeffect = list(int_classroom = list(variance = 5, var_level = 2)),
    propensity = list(
        formula = trt ~ 1 + age + ses + (1 | classroom),
        fixed = list(age = list(var_type = 'ordinal', 
                         levels = -7:7),
                     ses = list(var_type = 'continuous', 
                         mean = 0, sd = 5, 
                         var_level = 2)),
        sample_size = list(level1 = level1_samp, level2 = 75),
        error = list(variance = 10),
        randomeffect = list(int_classroom = list(variance = 5, var_level = 2)),
        reg_weights = c(2, 0.5, -0.8),
        outcome_type = 'binary',
        outcome_level = 2
    ),
    model_fit = list(formula = achievement ~ 1 + motivation + trt + (1 | classroom),
                   model_function = lme4::lmer),
    propensity_model = list(
        formula = trt ~ 1 + age + ses + (1 | classroom),
        propensity_type = 'covariate',
        model_function = lme4::glmer,
        propensity_model_args = list(
           family = binomial()
        )
    ),
    replications = 10,
    extract_coefficients = TRUE
)

replicate_simulation(sim_arguments)
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge with max|grad| = 0.0556873 (tol = 0.002, component 1)
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, : Model is nearly unidentifiable: very large eigenvalue
 - Rescale variables?
[[1]]
         term      estimate    std.error statistic
1 (Intercept)  2.908904e+00 7.138991e-01  4.074670
2  motivation  4.056633e-01 4.302511e-03 94.285228
3         trt  2.369709e+04 6.787640e+03  3.491212
4  propensity -2.369950e+04 6.788101e+03 -3.491329

[[2]]
         term      estimate    std.error statistic
1 (Intercept)  1.256255e+00 4.501801e-01  2.790561
2  motivation  3.988186e-01 4.456008e-03 89.501326
3         trt  1.035445e+04 6.851057e+03  1.511366
4  propensity -1.035536e+04 6.851238e+03 -1.511458

[[3]]
         term      estimate    std.error statistic
1 (Intercept)  9.734051e-01 5.325444e-01  1.827838
2  motivation  4.034641e-01 4.247209e-03 94.995117
3         trt  1.522479e+04 9.038478e+03  1.684441
4  propensity -1.522510e+04 9.038724e+03 -1.684430

[[4]]
         term      estimate    std.error statistic
1 (Intercept)     1.2694900 4.291298e-01  2.958289
2  motivation     0.3971322 4.178960e-03 95.031348
3         trt  5118.1511922 3.557972e+03  1.438502
4  propensity -5118.8380437 3.558231e+03 -1.438591

[[5]]
         term      estimate    std.error  statistic
1 (Intercept)     1.4644805 5.567131e-01  2.6305841
2  motivation     0.3982062 4.077144e-03 97.6679352
3         trt  2105.2649994 7.100847e+03  0.2964808
4  propensity -2106.0079375 7.101062e+03 -0.2965765

[[6]]
         term      estimate    std.error statistic
1 (Intercept)     0.8776863 5.054796e-01  1.736343
2  motivation     0.3955913 4.261973e-03 92.818811
3         trt  3796.5598590 2.271809e+03  1.671162
4  propensity -3797.5932828 2.272149e+03 -1.671367

[[7]]
         term      estimate    std.error statistic
1 (Intercept)     1.1598000 4.936926e-01  2.349235
2  motivation     0.4055483 4.287862e-03 94.580542
3         trt  6389.5839804 2.894362e+03  2.207597
4  propensity -6390.3572335 2.894661e+03 -2.207636

[[8]]
         term      estimate    std.error statistic
1 (Intercept)  2.024031e+00 4.310026e-01  4.696100
2  motivation  4.006582e-01 4.150963e-03 96.521753
3         trt  1.704448e+04 6.978264e+03  2.442510
4  propensity -1.704617e+04 6.978520e+03 -2.442663

[[9]]
         term      estimate    std.error statistic
1 (Intercept)  1.001839e+00 5.212012e-01  1.922172
2  motivation  4.024457e-01 4.201464e-03 95.786999
3         trt  1.776691e+04 8.062954e+03  2.203524
4  propensity -1.776733e+04 8.063197e+03 -2.203509

[[10]]
         term      estimate    std.error statistic
1 (Intercept)  2.475772e+00 6.106023e-01  4.054639
2  motivation  4.004046e-01 4.167494e-03 96.078010
3         trt  1.989337e+04 7.453907e+03  2.668851
4  propensity -1.989594e+04 7.454200e+03 -2.669091

Bayesian Model Fitting with brms

It is also possible to use different model fitting functions. For example, if you wanted to use a Bayesian logistic regression function, this is now possible with the new model fitting functionality. I’m going to use the example from the last post with single level propensity score models to demonstrate this feature. Here, I will use the brms::brm() function to fit a Bayesian logistic regression model for the propensity score model.

Code 
sim_arguments <- list(
    formula = achievement ~ 1 + motivation + trt + age + ses,
    fixed = list(
        motivation = list(var_type = 'continuous',
                           mean = 0, sd = 20)
    ),
    sample_size = 400,
    error = list(variance = 10),
    reg_weights = c(50, 0.4, 1.2, 0.1, 0.25),
    propensity = list(
        formula = trt ~ 1 + age + ses,
        fixed = list(age = list(var_type = 'ordinal', 
                         levels = -7:7),
                     ses = list(var_type = 'continuous', 
                         mean = 0, sd = 5)),
        sample_size = 400,
        error = list(variance = 5),
        reg_weights = c(2, 0.3, -0.5),
        outcome_type = 'binary'
    ),
    model_fit = list(formula = achievement ~ 1 + motivation + trt + age + ses,
                   model_function = 'lm'),
    propensity_model = list(
        formula = trt ~ 1 + age + ses,
        propensity_type = 'sbw',
        model_function = brms::brm,
    propensity_model_args = list(iter = 250, chains = 2, family = brms::bernoulli())
    ),
    replications = 2,
    extract_coefficients = TRUE
)
replicate_simulation(sim_arguments) 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 2.2e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.22 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: WARNING: There aren't enough warmup iterations to fit the
Chain 1:          three stages of adaptation as currently configured.
Chain 1:          Reducing each adaptation stage to 15%/75%/10% of
Chain 1:          the given number of warmup iterations:
Chain 1:            init_buffer = 18
Chain 1:            adapt_window = 95
Chain 1:            term_buffer = 12
Chain 1: 
Chain 1: Iteration:   1 / 250 [  0%]  (Warmup)
Chain 1: Iteration:  25 / 250 [ 10%]  (Warmup)
Chain 1: Iteration:  50 / 250 [ 20%]  (Warmup)
Chain 1: Iteration:  75 / 250 [ 30%]  (Warmup)
Chain 1: Iteration: 100 / 250 [ 40%]  (Warmup)
Chain 1: Iteration: 125 / 250 [ 50%]  (Warmup)
Chain 1: Iteration: 126 / 250 [ 50%]  (Sampling)
Chain 1: Iteration: 150 / 250 [ 60%]  (Sampling)
Chain 1: Iteration: 175 / 250 [ 70%]  (Sampling)
Chain 1: Iteration: 200 / 250 [ 80%]  (Sampling)
Chain 1: Iteration: 225 / 250 [ 90%]  (Sampling)
Chain 1: Iteration: 250 / 250 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.004 seconds (Warm-up)
Chain 1:                0.003 seconds (Sampling)
Chain 1:                0.007 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 6e-06 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.06 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: WARNING: There aren't enough warmup iterations to fit the
Chain 2:          three stages of adaptation as currently configured.
Chain 2:          Reducing each adaptation stage to 15%/75%/10% of
Chain 2:          the given number of warmup iterations:
Chain 2:            init_buffer = 18
Chain 2:            adapt_window = 95
Chain 2:            term_buffer = 12
Chain 2: 
Chain 2: Iteration:   1 / 250 [  0%]  (Warmup)
Chain 2: Iteration:  25 / 250 [ 10%]  (Warmup)
Chain 2: Iteration:  50 / 250 [ 20%]  (Warmup)
Chain 2: Iteration:  75 / 250 [ 30%]  (Warmup)
Chain 2: Iteration: 100 / 250 [ 40%]  (Warmup)
Chain 2: Iteration: 125 / 250 [ 50%]  (Warmup)
Chain 2: Iteration: 126 / 250 [ 50%]  (Sampling)
Chain 2: Iteration: 150 / 250 [ 60%]  (Sampling)
Chain 2: Iteration: 175 / 250 [ 70%]  (Sampling)
Chain 2: Iteration: 200 / 250 [ 80%]  (Sampling)
Chain 2: Iteration: 225 / 250 [ 90%]  (Sampling)
Chain 2: Iteration: 250 / 250 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 0.004 seconds (Warm-up)
Chain 2:                0.003 seconds (Sampling)
Chain 2:                0.007 seconds (Total)
Chain 2: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 1.8e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.18 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: WARNING: There aren't enough warmup iterations to fit the
Chain 1:          three stages of adaptation as currently configured.
Chain 1:          Reducing each adaptation stage to 15%/75%/10% of
Chain 1:          the given number of warmup iterations:
Chain 1:            init_buffer = 18
Chain 1:            adapt_window = 95
Chain 1:            term_buffer = 12
Chain 1: 
Chain 1: Iteration:   1 / 250 [  0%]  (Warmup)
Chain 1: Iteration:  25 / 250 [ 10%]  (Warmup)
Chain 1: Iteration:  50 / 250 [ 20%]  (Warmup)
Chain 1: Iteration:  75 / 250 [ 30%]  (Warmup)
Chain 1: Iteration: 100 / 250 [ 40%]  (Warmup)
Chain 1: Iteration: 125 / 250 [ 50%]  (Warmup)
Chain 1: Iteration: 126 / 250 [ 50%]  (Sampling)
Chain 1: Iteration: 150 / 250 [ 60%]  (Sampling)
Chain 1: Iteration: 175 / 250 [ 70%]  (Sampling)
Chain 1: Iteration: 200 / 250 [ 80%]  (Sampling)
Chain 1: Iteration: 225 / 250 [ 90%]  (Sampling)
Chain 1: Iteration: 250 / 250 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.004 seconds (Warm-up)
Chain 1:                0.003 seconds (Sampling)
Chain 1:                0.007 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 5e-06 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: WARNING: There aren't enough warmup iterations to fit the
Chain 2:          three stages of adaptation as currently configured.
Chain 2:          Reducing each adaptation stage to 15%/75%/10% of
Chain 2:          the given number of warmup iterations:
Chain 2:            init_buffer = 18
Chain 2:            adapt_window = 95
Chain 2:            term_buffer = 12
Chain 2: 
Chain 2: Iteration:   1 / 250 [  0%]  (Warmup)
Chain 2: Iteration:  25 / 250 [ 10%]  (Warmup)
Chain 2: Iteration:  50 / 250 [ 20%]  (Warmup)
Chain 2: Iteration:  75 / 250 [ 30%]  (Warmup)
Chain 2: Iteration: 100 / 250 [ 40%]  (Warmup)
Chain 2: Iteration: 125 / 250 [ 50%]  (Warmup)
Chain 2: Iteration: 126 / 250 [ 50%]  (Sampling)
Chain 2: Iteration: 150 / 250 [ 60%]  (Sampling)
Chain 2: Iteration: 175 / 250 [ 70%]  (Sampling)
Chain 2: Iteration: 200 / 250 [ 80%]  (Sampling)
Chain 2: Iteration: 225 / 250 [ 90%]  (Sampling)
Chain 2: Iteration: 250 / 250 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 0.004 seconds (Warm-up)
Chain 2:                0.004 seconds (Sampling)
Chain 2:                0.008 seconds (Total)
Chain 2: 
[[1]]
# A tibble: 5 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)   50.4     0.405      124.   5.47e-319
2 motivation     0.410   0.00830     49.4  3.16e-171
3 trt            0.542   0.514        1.05 2.92e-  1
4 age            0.152   0.0456       3.33 9.58e-  4
5 ses            0.194   0.0350       5.54 5.39e-  8

[[2]]
# A tibble: 5 × 5
  term        estimate std.error statistic   p.value
  <chr>          <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)   50.6     0.379     133.    0        
2 motivation     0.405   0.00855    47.3   7.05e-165
3 trt            0.288   0.474       0.606 5.45e-  1
4 age            0.109   0.0435      2.52  1.23e-  2
5 ses            0.159   0.0402      3.96  9.02e-  5

⚙️ Note: For demonstration purposes, this example uses only 2 replications and 250 iterations across 2 chains. For accurate estimation, these should be increased substantially.

Conclusion

These enhancements make simglm a more powerful framework for propensity score simulation, causal inference, and power analysis in multi-level contexts. You can now simulate, estimate, and evaluate designs involving cluster-level assignment, cross-level effects, and complex hierarchical data structures—all within a single pipeline!